Use a hex editor
From Sonic Retro
(Redirected from SCHG How-to:Use a Hex Editor)
(Original guide by Scarred Sun)
Contents
What is hex?
When you program something--anything--what you essentially are doing are setting a series of switches for something. Think of a lamp. When you flip the switch, the light comes on; when you flip it off, it goes off. We'll assign the lamp the number 1 when it's switched on and the number 0 when it's off. This is binary; only two numbers exist in our lamp-numbering world.
Now, let's say you have four lamps, all that have switches on them.
1 2 3 4
Any of these can be on or off at any time. If you think back to elementary school math, you can figure out that that leaves 16 possibilities for different on/off combinations. Remember how we assigned 1 to on and 0 to off? Let's say we turn all four lamps on. That would leave us with 1111 to represent the lamps.
This is how all things are programmed--by a series of small switches that add up to show bigger pictures. However, it'd be really long, arduous and confusing to type out nothing but 0 and 1s all day! Therefore, rather than noting things simply by one on/off switch over and over, that can be compressed by using base 16 counting. We normally use base 10, or decimal, counting--0, 1, 2, 3, 4, 5, 6, 7, 8, 9--to represent what our core numbers are. Base 16, also known as hexa (six) decimal (ten) to count higher by adding six letters afterwards. Basically, you would count as 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, etc. You'll notice this counting in places like Sonic 2's sound test.
So, let's go back to the lamps. We have sixteen different combinations, right? That's the same number as hex! Therefore, we can shorten the on/off expression by using hex.
To get there, we'll now assign each lamp a number. So what was
1 2 3 4
now becomes
8 4 2 1
So if we express that lamps 2 and 1 are on, we'd write
0 0 1 1 . 2+1 = 3. 3 is the hexadecimal value for this combination. In the case of all four lamps being on, like earlier, we'd write
1 1 1 1. 8+4+2+1 = 15. So count this up in hexadecimal, rather than in binary, and you get F.
SCHG:Number Systems has a little more on this concept, along with a quick chart to show how numbers convert between binary, decimal, and hexadecimal.
How is this relevant to Sonic hacking?
When you take a Sonic ROM, you'll notice that it's either named .bin or .smd. .bin refers to binary files--all these switches compiled into one large document! .smd, on the other hand, rearranges the binary files in another format, and that's why when you do any hacking, all your files need to be in straight .bin format.
So, when you open a .bin file in a hex editor, you see the hex values for all these switches. There are lots of hex editors out there--literally dozens, and you can spend some time playing around with different ones. A lot of hackers like Hex Workshop, because it has a lot of advanced features, but at the end of the day, you're simply changing hex values. Hex Workshop is not free software; you would need to buy it in order to use it. However, there are loads of free hex editors. For this topic, I'll be using ICY Hexplorer, a free and simple hex editor that should handle most day-to-day edits.
Why and when should I edit hex?
Before the advent of Sonic hacking utilities, hex editing was the only way to edit a ROM. In fact, that's simply what hacking programs do today--they're a graphical frontend to changing these values around. However, there are still things that these programs cannot do, areas where they glitch up required hex values and you'll need to manually fix them, and just having a sense of what's going on under the hood can help you be a better hacker. Hex is relevant to many parts of the hacking scene. For instance, IPS patches are just a piece of code saying to change certain hex values to another piece of code.
However, if you are working with ASM, hex becomes a totally different beast, because you are placing your hex values in different order than the normal ROM. If you insert an extra level, for instance, your code will no longer line up with a regular ROM--that's why most modern hacks, which use ASM, distribute them as full ROMs rather than IPS patches, because all the data is shifting and moving around, not just a set of values!
OK, I'm interested. Now what?
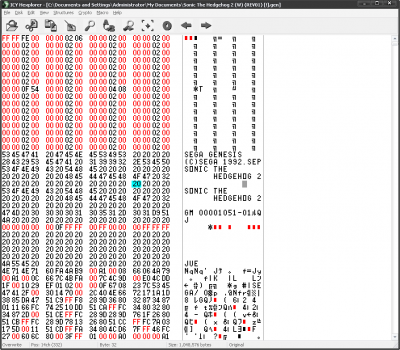
Open up your hex editor and load your ROM. For this topic, I'll be loading up a Sonic 2 Final ROM. You should see something like this:
On your left, you'll see the hex values for for the code; on the right, the ASCII equivalents are shown. In some games, like Sonic Spinball, things like text are, in fact, stored in ASCII format; however, most games use a form of compression or encryption instead.
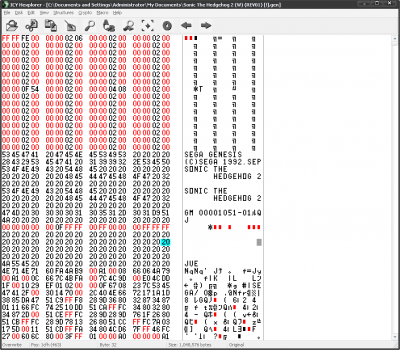
Now, highlight the bottom-right hex value by clicking on it.
You'll notice in the bottom status bar that there's something saying "Pos: 1cfh" This is the number in hex where that value is stored--it's the 1CFth value, so to speak. This is what's commonly called the hex offset. In order to find where values are, you use the offset.
For years, hackers have worked diligently to figure out what value is at what offset. Over the years, this information was gathered up in what you all know as the Sonic Community Hacking Guide for the games. Now, since we're using Sonic 2, let's open up SCHG:Sonic 2 and take a look at "Game Configuration."
$3C79: Starting lives for player 1
Using this value, we can change the amount of lives that Sonic starts with in the game. So, let's go to that offset! Select View->Go To Address (or press F5), and you'll get a small dialog box. In offset, type in 3C79. Make sure "hexadecimal" is selected as the base! The hex editor will take you to that value.
Here, you can see that the value for $3C79 is 03--the number of lives Sonic starts with in hex. Now, let's say we just really suck at Sonic 2 or something and want to make the number of lives that Sonic starts with to be, oh, 42.
If you type 42 there, you will NOT get 42 lives--you'll get 66! You'll need to write 42 in hexadecimal, which translates to 2A. So type 2A, and it will overwrite the previous value. Save and load your ROM up in an emulator. Sure enough, you'll have 42 lives!
This is a really simple example, but by using multiple hex values, you can do a LOT--just look around the S2 hacking guide to get an idea of the many possibilities.
And that, my friends, is how to edit a ROM using hexadecimal values. Happy hacking!